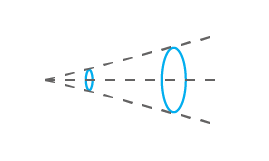
光斑尺寸和光束腰

首先，考虑有高斯激光穿过汇聚透镜。光束将开始汇聚，并最终达到最大浓度点。此时，光束直径将达到最小值。这个直径就是我们所说的“光斑尺寸”（“光束腰”也是同样的概念，但一般指半径）。过了腰部，光束又开始发散，而且越往后越宽。腰部在 Z 轴上的位置主要取决于焦距。从本质上讲，焦距是一个数值，表示透镜使光线汇聚或发散的程度。因此，透镜的汇聚程度越高，焦距就越小，腰部就越靠近镜头。因此，如果知道与光束腰的距离，就可以确定光束的大小。此外，所谓景深是指以光束腰为中心的特定距离，在这个距离内，光束的直径与其光斑尺寸相比明显较小。这也是瑞利距离的两倍。瑞利长度的定义是光束半径小于等于腰部半径 √2 倍的距离。因此，当焦距小于入射光束尺寸时，景深往往较小，反之亦然。最后，M² 相当于质量系数。基本来说，这是与形状完美的理论 TEM₀₀ 高斯光束相比，对于光束性能的测量。“1”的值被认为是完美的，离这个值越远，就越不完美。