Strahldivergenz und Durchmesser

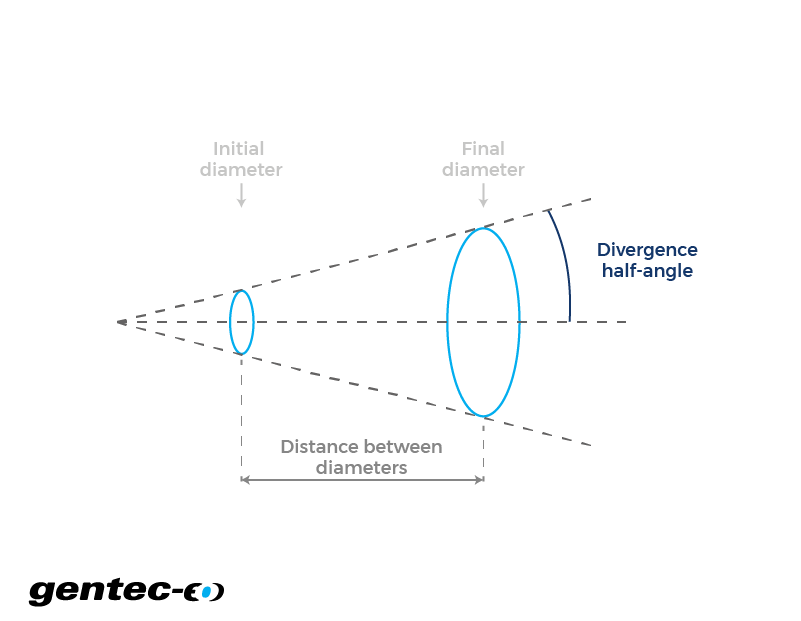
In der Optik bezieht sich die Laserstrahldivergenz darauf, wie stark sich ein Strahl über eine Entfernung ausbreitet. Stellen Sie sich einen Kegel vor, dessen Spitze der theoretische Ursprung des Laserstrahls ist (wo der Strahldurchmesser punktförmig wäre). Wenn Sie den Winkel zwischen zwei Vektoren messen, einer von der Kegelspitze zum Mittelpunkt der Basis und der zweite von der Kegelspitze zur Seite der Basis, ist der resultierende Winkel das, was man als Divergenz-Halbwinkel bezeichnet. Offensichtlich wäre der volle Winkel das Doppelte davon. Wenn man dann drei von vier Parametern kennt – Anfangsdurchmesser, Enddurchmesser, Abstand zwischen den Durchmessern und Divergenzwinkel – hat man alle notwendigen Informationen, um den vierten Parameter zu berechnen. Wenn man das Bild richtig versteht, wird man auch erkennen, dass der Anfangsdurchmesser tatsächlich jeder Durchmesser entlang der Z-Achse sein kann und nicht derjenige am Ausgang des Lasers sein muss.