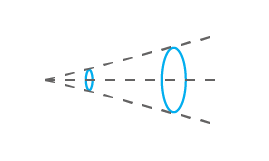
Spotgröße und Strahltaille

Betrachten wir zunächst einen Gaußschen Laserstrahl, der durch eine Sammellinse läuft. Der Strahl beginnt zu konvergieren und erreicht schließlich einen Punkt mit maximaler Konzentration. An diesem Punkt hat der Strahldurchmesser sein Minimum. Dieser Durchmesser wird als „Spotgröße“ bezeichnet (die „Strahltaille“ ist das gleiche Konzept, bezieht sich aber im Allgemeinen auf den Radius). Jenseits der Taille beginnt der Strahl wieder zu divergieren und wird mit zunehmender Entfernung breiter. Die Position der Taille auf der z-Achse hängt unter anderem von der Brennweite ab. Im Wesentlichen ist die Brennweite ein Wert, der angibt, wie stark eine Linse das Licht konvergieren oder divergieren lässt. Je stärker eine Linse konvergiert, desto kleiner ist die Brennweite und desto näher an der Linse befindet sich die Taille. Daher ist es möglich, die Größe des Strahls zu bestimmen, wenn der Abstand zur Strahltaille bekannt ist. Die sogenannte Tiefenschärfe ist der spezifische Abstand, zentriert um die Strahltaille, innerhalb dessen der Strahl einen im Verhältnis zu seiner Spotgröße bemerkenswert kleinen Durchmesser aufweist. Sie ist auch das Doppelte der Rayleigh-Distanz. Die Rayleigh-Länge ist definiert als der Abstand, bei dem der Strahlradius kleiner oder gleich dem √2-fachen des Radius an der Strahltaille ist. Wenn also die Brennweite im Vergleich zur Größe des einfallenden Strahls klein ist, ist die Schärfentiefe tendenziell klein und umgekehrt. M² schließlich entspricht dem Qualitätsfaktor. Im Grunde ist es ein Maß dafür, wie gut sich Ihr Strahl im Vergleich zu einem perfekt geformten theoretischen TEM₀₀ Gauß-Strahl verhält. Ein Wert von „1“ gilt als perfekt, und je weiter Sie von diesem Wert entfernt sind, desto weniger ist er es.