조리개 투과율
이 무료 온라인 계산기를 사용하여 조리개를 통과하는 레이저 빔 투과율을 계산하세요.
레이저 빔 조리개 계산기는 어떻게 작동하나요?
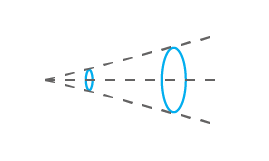
원형 가우스 레이저 빔을 고려할 경우, 이 빔이 생성하는 각 파면은 (이론적으로) 우주의 어디에서나 일정한 에너지 값을 가집니다. 따라서 레이저 빔이 조리개를 통과할 때 조리개가 실제로 아무리 크더라도 입사된 레이저 빔에서 통과하지 못하는 에너지가 일정량 존재합니다. 레이저 빔의 1/e²에서 직경을 알면 조리개를 통과하는 결과 출력을 계산할 수 있습니다. 예상할 수 있듯이 조리개가 클수록 차단되는 출력의 비율은 무시할 수 있을 정도로 낮아집니다. 이는 감지기를 사용할 때 중요한데, 조리개 치수가 부적절하면 출력이나 에너지가 부정확하게 측정될 수 있기 때문입니다. 이는 새로운 기술의 광학 설계를 고려할 때도 마찬가지입니다. 마지막으로, 측정의 정확도가 어느 정도까지 정확해야 하는지에 따라 (그리고 빔의 중심을 감지기에 얼마나 잘 맞추는지에 따라), 경험상 1/e²에서 빔 크기의 2배인 조리개를 사용하게 됩니다. 현시점에서 입사 빔 출력의 99.9% 이상이 조리개를 통과합니다. (완벽하게 중앙에 위치한 경우).
확대하려면
클릭

공식
공식은 완벽한 원형 가우스 레이저 빔의 거동을 설명합니다. 따라서 실제 조건에서 얻을 수 있는 값의 근사치를 나타냅니다. 빔에 사용되는 직경 값은 1/e² 파라미터입니다. 또한 레이저 빔이 조리개의 중앙에 완벽하게 위치하여 빔과 조리개가 두 개의 동심원을 이룬다고 가정합니다. 또한 가우스 빔의 지름은 z의 함수임을 숙지해야 합니다. 따라서 측정하는 지점에 따라 그 값이 달라집니다. 이는 공간에서 가우스 빔의 전파에 관한 보다 복잡한 물리적 개념이므로 여기서는 다루지 않습니다.
참조: Saleh, B. E. A., & Teich, M. C. (2007). Fundamentals of Photonics (2nd ed.). Wiley-Interscience.
복사하려면
우클릭
복사하려면
우클릭