빔 발산과 직경
이 온라인 계산기를 사용하여 레이저 빔 발산(반각)과 직경을 편리하게 계산하세요.
레이저 빔 발산과 직경 계산기는 어떻게 작동하나요?
광학에서 레이저 빔 발산이란 빔이 거리에 따라 얼마나 퍼지는지를 나타냅니다. 원뿔의 끝이 레이저 빔의 이론적 원점(빔 직경이 정확히 일치하는 지점)이라고 상상해 보세요. 하나는 원뿔의 끝에서 밑변의 중심으로 향하는 벡터와 다른 하나는 원뿔의 끝에서 밑변의 측면으로 향하는 두 벡터가 있고 그 사이의 각도를 측정한 결과로 나온 각도를 발산 반각이라고 부를 수 있습니다. 당연히 전체 각도는 그 두 배가 될 것입니다. 그런 다음 초기 직경, 최종 직경, 직경 사이의 거리, 발산 각도라는 네 가지 매개변수 중 세 가지만 알면 네 번째 매개변수를 계산하는 데 필요한 모든 정보를 얻은 셈이 됩니다. 또한 그림을 명확하게 이해한다면 초기 직경은 실제로 Z축을 따라 임의의 직경이 될 수 있으며 레이저 출구의 직경일 필요가 없음을 알 수 있습니다.
확대하려면
클릭
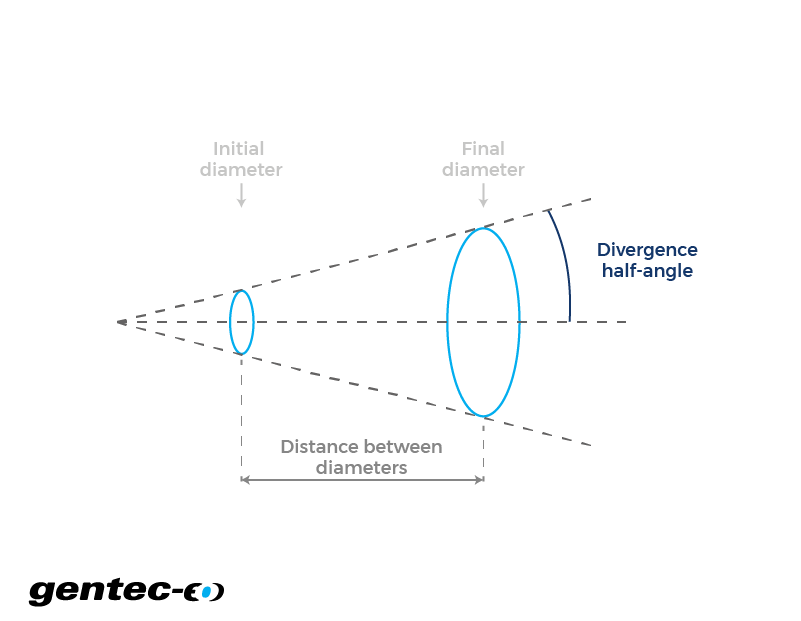
레이저 빔 직경과 발산 공식
모든 레이저 계산기에서는 빔이 완벽한 TEM₀₀ 가우스 빔의 형태이며 발산이 일정하다고 가정합니다. 이는 두 직경이 모두 동일한 균질성과 연속적인 등방성 매질 내부에 있다고 가정한다는 것을 의미합니다. 그렇지 않으면 발산은 공간의 함수가 되므로 일정하지 않습니다. 이 방정식을 사용하여 레이저 빔 직경과 발산(반각)을 계산할 수 있습니다.
참조: Saleh, B. E. A., & Teich, M. C. (2007). Fundamentals of Photonics (2nd ed.). Wiley-Interscience.
복사하려면
우클릭
복사하려면
우클릭