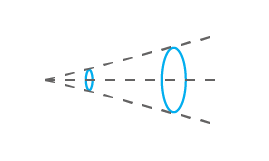
스팟 크기와 빔 웨이스트

먼저 수렴 렌즈를 통과하는 가우스 레이저 빔을 생각해 보겠습니다. 빔이 수렴하기 시작하여 결국 최대 농도 지점에 도달하게 됩니다. 이 시점에서 빔 직경은 최소가 됩니다. 이 지름을 "스팟 크기"라고 합니다("빔 웨이스트"는 같은 개념이지만 일반적으로 반경을 나타냅니다). 웨이스트 지점을 지나면 빔이 다시 발산하기 시작하고 더 멀리 갈수록 더 넓어집니다. Z축의 웨이스트 위치는 무엇보다 초점 거리에 따라 달라집니다. 기본적으로 초점 거리는 렌즈가 빛을 얼마나 강하게 수렴 또는 발산하게 하는지를 나타내는 값입니다. 따라서 렌즈가 더 많이 수렴할수록 초점 거리가 짧아지고 웨이스트가 렌즈에 더 가까워집니다. 따라서 빔 웨이스트로부터의 거리를 알면 빔의 크기를 결정할 수 있습니다. 또한 초점 심도라고 하는 것은 빔 웨이스트를 중심으로 한 특정 거리로, 스팟 크기에 비해 빔의 직경이 현저히 작은 경우입니다. 이는 또한 레일리 거리의 두 배에 달합니다. 레일리 길이는 빔 반경이 웨이스트에서 반경의 √2배보다 작거나 같은 거리로 정의합니다. 따라서 입사 빔 크기에 비해 초점 거리가 작으면 초점 심도가 작아지고 그 반대의 경우도 마찬가지입니다. 마지막으로 M²는 품질 계수입니다. 기본적으로 완벽한 형태의 이론적 TEM₀₀ 가우스 빔과 비교했을 때 빔이 얼마나 잘 작동하는지를 측정하는 것입니다. "1"이란 값은 완벽한 것으로 간주되며, 이 값에서 멀어질수록 완벽하지 않은 것으로 간주됩니다.