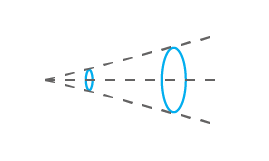
Aperture transmission

When you consider a circular Gaussian laser beam, each wavefront that it creates has (theoretically) a certain value of energy everywhere in the universe. So, if the laser beam goes through an aperture, no matter how big the aperture actually is, there is a certain amount of energy from the incident laser beam that does not go through. Knowing the diameter at 1/e² of your laser beam will then make it possible to calculate the resulting power that is passing through an aperture. As one could expect, the bigger the aperture, the more negligible becomes the proportion of the power that is blocked. This is of importance when using detectors, mainly because having an inappropriate aperture dimension would lead to inaccurate measurements of either power or energy. This is also true when thinking about optical designs of new technologies. Finally, depending on how crucial your accuracy of measurement needs to be (and how good you are at centering your beam on the detector), as a rule of thumb, aim for an aperture that is double the size of the beam at 1/e². At this point, you’ll already have more than 99.9% of that incident beam power going through the aperture (if perfectly centered).